Company dynamics

NLP实战篇之bert源码阅读（optimization）

本文主要会阅读bert源码（https://github.com/google-research/bert ）中的optimization.py文件，已完成modeling.py、run_pretraining.py文件的源码阅读，后续会陆续阅读bert的数据准备、下游任务训练等源码等。本文大体以优化算法中各个概念为基础介绍optimization.py，先后介绍了学习率的衰减、学习率预热、权重衰减、Adam算法，以及作者自己添加的Adam矩估计校正。

实战系列篇章中主要会分享，解决实际问题时的过程、遇到的问题或者使用的工具等等。如问题分解、bug排查、模型部署等等。相关代码实现开源在：https://github.com/wellinxu/nlp_store ，更多内容关注知乎专栏（或微信公众号）：NLP杂货铺。

学习率衰减
学习率预热
权重衰减
Adam算法
矩估计校正

学习率在梯度下降类优化算法中有着特别重要的作用，学习率越大会使权重更新越快。大的学习率虽然能够让模型较快收敛，但也会引起模型震荡，从而错过更优解。所以通常情况下，我们希望学习率在一开始大一些，让权重快速收敛，然后再小一些，可以让模型得到一个更优的解空间。optimization.py中就使用了线性学习率衰减来达到这个目的，其中相关代码为：

# 实现学习率的线性衰减
learning_rate = tf.train.polynomial_decay(
      learning_rate,
      global_step,
      num_train_steps,
      end_learning_rate=0.0,
      power=1.0,
      cycle=False)

具体公式是：

$lr=(lr-end\\_learning\\_rate)*(1-global\\_step/num\\_train\\_steps)^{power}+end\\_learning\\_rate \\\\$

这里其实是多项式衰减，因为power等于1，所以变成线性衰减。学习率线性衰减的过程大概如下图所示：

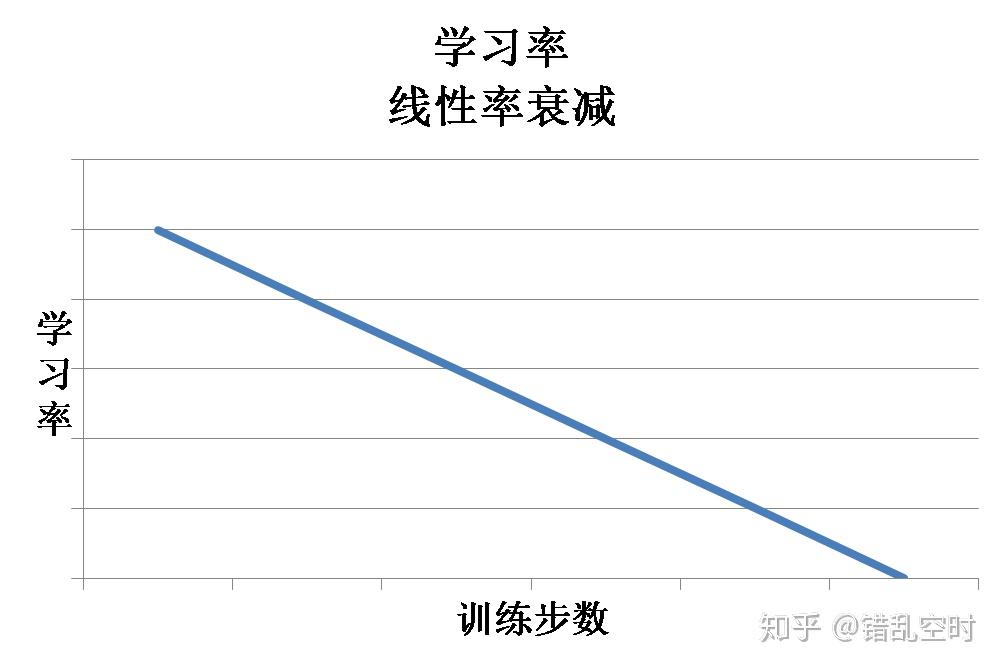
学习率预热是指在训练初期选择一个较小的学习率，然后在训练一定步数之后使用预先设置好的学习率。因为刚开始的时候模型是随机初始化权重，如果使用较大的学习率，会让模型不稳定，所以可以在一定训练步数内，使用较小的学习率，模型可以慢慢稳定，然后使用之前设定的学习率。这种情况下，学习率走势如下图所示：

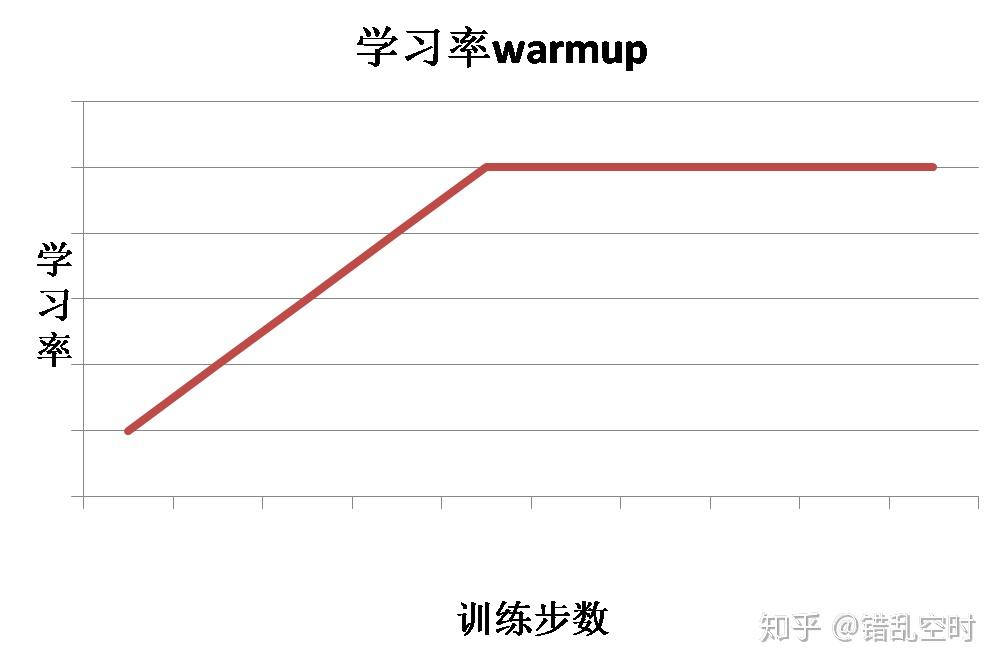
具体代码如下：

# 实现线性warmup.
  # 如果global_step < num_warmup_steps
  # 那么学习率为`global_step/num_warmup_steps * init_lr`.
  if num_warmup_steps:
    global_steps_int = tf.cast(global_step, tf.int32)
    warmup_steps_int = tf.constant(num_warmup_steps, dtype=tf.int32)

    global_steps_float = tf.cast(global_steps_int, tf.float32)
    warmup_steps_float = tf.cast(warmup_steps_int, tf.float32)

    warmup_percent_done = global_steps_float / warmup_steps_float    # 线性比例
    warmup_learning_rate = init_lr * warmup_percent_done    # 线性比例的学习率

    is_warmup = tf.cast(global_steps_int < warmup_steps_int, tf.float32)    # 是否在预热阶段
    # 如果在预热阶段，学习率就为warmup_learning_rate，否则为learning_rate
    # 一般是先上升后下降，因为learning_rate本身会线性衰减
    learning_rate = (
        (1.0 - is_warmup) * learning_rate + is_warmup * warmup_learning_rate)

optimization.py中则是将学习率预热与衰减结合在一起使用，在一定训练步数内进行学习率预热，然后就开始学习率衰减，这样结合的效果如下图所示：

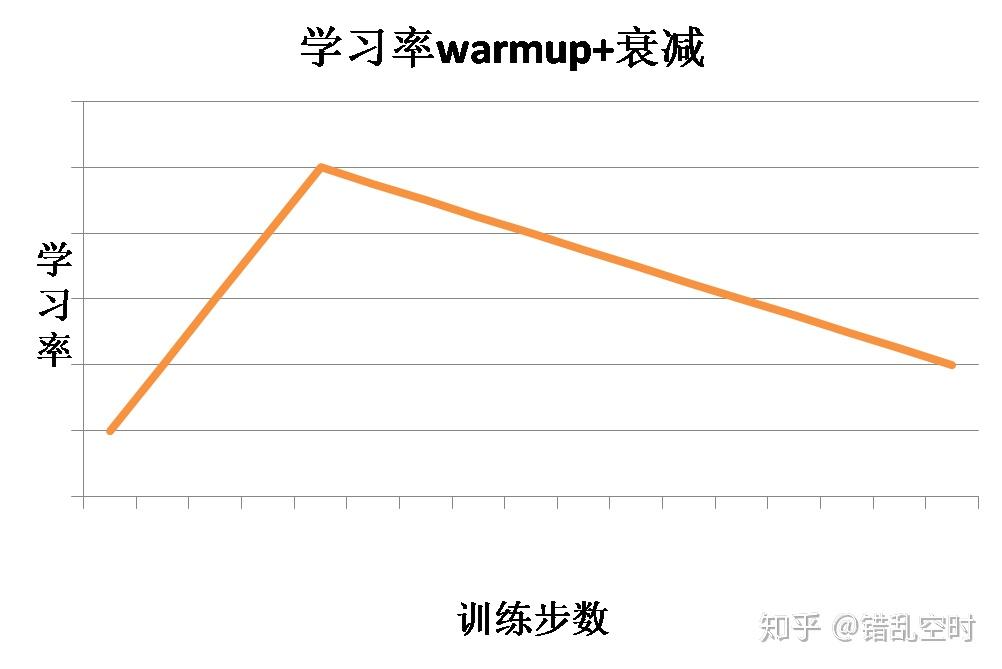
这样学习率先进过预热再进行衰减，代入Adam优化算法中，就实现了BERT的优化工作，整体代码如下所示：

def create_optimizer(loss, init_lr, num_train_steps, num_warmup_steps, use_tpu):
  """
  创建优化器训练操作optimizer training op.
  :param loss: loss值
  :param init_lr: int，初始学习率
  :param num_train_steps: int，训练总步数
  :param num_warmup_steps: int，预热步数
  :param use_tpu: bool，是否使用TPU
  :return: 训练中优化参数时需要进行的操作
  """
  global_step = tf.train.get_or_create_global_step()    # 获取当前步数

  learning_rate = tf.constant(value=init_lr, shape=[], dtype=tf.float32)    # 学习率初始化值

  # 实现学习率的线性衰减
  learning_rate = tf.train.polynomial_decay(
      learning_rate,
      global_step,
      num_train_steps,
      end_learning_rate=0.0,
      power=1.0,
      cycle=False)

  # 实现线性warmup.
  # 如果global_step < num_warmup_steps
  # 那么学习率为`global_step/num_warmup_steps * init_lr`.
  if num_warmup_steps:
    global_steps_int = tf.cast(global_step, tf.int32)
    warmup_steps_int = tf.constant(num_warmup_steps, dtype=tf.int32)

    global_steps_float = tf.cast(global_steps_int, tf.float32)
    warmup_steps_float = tf.cast(warmup_steps_int, tf.float32)

    warmup_percent_done = global_steps_float / warmup_steps_float    # 线性比例
    warmup_learning_rate = init_lr * warmup_percent_done    # 线性比例的学习率

    is_warmup = tf.cast(global_steps_int < warmup_steps_int, tf.float32)    # 是否在预热阶段
    # 如果在预热阶段，学习率就为warmup_learning_rate，否则为learning_rate
    # 一般是先上升后下降，因为learning_rate本身会线性衰减
    learning_rate = (
        (1.0 - is_warmup) * learning_rate + is_warmup * warmup_learning_rate)

  # 推荐使用这个优化器来进行微调，因为预训练是用这个训练的
  # (要注意Adam中的变量m/v不是从init_checkpoint中加载来的)
  optimizer = AdamWeightDecayOptimizer(
      learning_rate=learning_rate,
      weight_decay_rate=0.01,
      beta_1=0.9,
      beta_2=0.999,
      epsilon=1e-6,
      exclude_from_weight_decay=["LayerNorm", "layer_norm", "bias"])

  if use_tpu:   # TPU时使用的优化器
    optimizer = tf.contrib.tpu.CrossShardOptimizer(optimizer)

  tvars = tf.trainable_variables()    # 可训练的变量
  grads = tf.gradients(loss, tvars)    # 计算各变量对loss的梯度

  # 梯度裁剪，预训练就是这样的
  (grads, _) = tf.clip_by_global_norm(grads, clip_norm=1.0)

  # 获取参数优化当中需要的操作算子
  train_op = optimizer.apply_gradients(
      zip(grads, tvars), global_step=global_step)

  # 通常情况下global_step的更新应该在`apply_gradients`方法中进行.
  # 但是`AdamWeightDecayOptimizer`中并没有完成这一步 doesn't do this. But if you use
  # 如果使用其他优化器，可能需要移除这一步
  new_global_step = global_step + 1
  train_op = tf.group(train_op, [global_step.assign(new_global_step)])
  return train_op

optimization.py中实现的Adam算法带了权重衰减（L2正则化），但是并没有直接将L2约束添加到loss函数中去，因为这样会影响Adam中梯度的一阶和二阶矩估计，所以使用了权重衰减的方式来处理，类似于在SGD中直接加上L2正则化，具体地，就是在每次权重更新时，进行一定比例的衰减，如下所示：

# 对于Adam算法来说，如果直接将权重的平方加到loss函数上，这不是正确的
      # L2正则化（权重衰减）方法，因为这样会影响Adam中m与v的计算。
      #
      # 我们需要一种不影响m/v参数的权重衰减方法，这里讲loss的优化与L2正则
      # 分开计算，先根据Adam算法计算针对loss需要更新的量，然后加上L2正则
      # 需要改变的量.
      if self._do_use_weight_decay(param_name):
        update += self.weight_decay_rate * param     # L2正则化（权重衰减）

当然也不是所有的参数都需要进行权重衰减的，代码中使用参数名来控制，首先使用_get_variable_name方法来获取变量名：

  def _get_variable_name(self, param_name):
    """从张量名字中获取变量名字"""
    m = re.match("^(.*):\\\\d+$", param_name)
    if m is not None:
      param_name = m.group(1)   # 获取正则表达式中第一个括号中的内容
    return param_name

然后再使用_do_use_weight_decay方法来判断是否要进行权重衰减。

  def _do_use_weight_decay(self, param_name):
    """判断名为param_name的变量是否要使用L2权重衰减（L2正则化）"""
    if not self.weight_decay_rate:
      return False
    if self.exclude_from_weight_decay:
      # 判断变量名是否在不需要做权重衰减的名单里
      for r in self.exclude_from_weight_decay:
        if re.search(r, param_name) is not None:
          return False
    return True

代码中，层标准化相关参数与偏置bias相关参数不进行权重衰减。

下图中显示了几个不同优化算法的迭代路线，Adam算法则是结合了Adagrad算法与Rmsprop算法的优点：

optimization.py中最核心的部分就是Adam相关算法的实现了，其具体公式如下所示：

$g=gradient(loss, p) \\\\$ $m_t=g(1-\\beta_1)+m_{t-1}\\beta_1 \\\\$ $\\\\ v_t=g^2(1-\\beta_2)+v_{t-1}\\beta_2$ $p=p - lr * \\frac{m_t}{\\sqrt{v_t}}\\\\$

其中gradient表示梯度计算函数，p为参数，g是p相对于loss的梯度， $m_t$ 是第t步是梯度的一阶矩估计， $v_t$ 是第t步时梯度的二阶矩估计。 $\\beta_1,\\beta_2$ 是常量参数。

所以，相关代码实现为：

class AdamWeightDecayOptimizer(tf.train.Optimizer):
  """包含修正L2正则化（权重衰减）的Adam优化器"""

  def __init__(self,
               learning_rate,
               weight_decay_rate=0.0,
               beta_1=0.9,
               beta_2=0.999,
               epsilon=1e-6,
               exclude_from_weight_decay=None,
               name="AdamWeightDecayOptimizer"):
    """
    创建一个Adam权重衰减优化器
    :param learning_rate: float，学习率
    :param weight_decay_rate: float，权重衰减比率
    :param beta_1: float， 默认0.9，梯度一阶矩估计用的参数
    :param beta_2: float， 默认0.999，梯度二阶矩估计用的参数
    :param epsilon: float，防止程序计算除0
    :param exclude_from_weight_decay: list，不需要L2正则化（权重衰减）的参数名称
    :param name: str，优化器名称
    """
    super(AdamWeightDecayOptimizer, self).__init__(False, name)

    self.learning_rate = learning_rate
    self.weight_decay_rate = weight_decay_rate
    self.beta_1 = beta_1
    self.beta_2 = beta_2
    self.epsilon = epsilon
    self.exclude_from_weight_decay = exclude_from_weight_decay
    # 笔者自己添加的变量
    self.beta_1_t = 1.0    # 用于修正一阶矩估计
    self.beta_2_t = 1.0    # 用于修正二阶矩估计

  def apply_gradients(self, grads_and_vars, global_step=None, name=None):
    """实现Adam梯度更新算法"""
    assignments = []
    # 循环各个变量与梯度
    for (grad, param) in grads_and_vars:
      if grad is None or param is None:
        continue

      param_name = self._get_variable_name(param.name)    # 获变量的名字

      # 获取梯度的一阶矩估计
      m = tf.get_variable(
          name=param_name + "/adam_m",
          shape=param.shape.as_list(),
          dtype=tf.float32,
          trainable=False,
          initializer=tf.zeros_initializer())
      # 获取梯度的二阶矩估计
      v = tf.get_variable(
          name=param_name + "/adam_v",
          shape=param.shape.as_list(),
          dtype=tf.float32,
          trainable=False,
          initializer=tf.zeros_initializer())

      # 梯度的一阶矩与二阶矩估计更新
      next_m = (
          tf.multiply(self.beta_1, m) + tf.multiply(1.0 - self.beta_1, grad))
      next_v = (
          tf.multiply(self.beta_2, v) + tf.multiply(1.0 - self.beta_2,
                                                    tf.square(grad)))

      update = next_m / (tf.sqrt(next_v) + self.epsilon)   # 梯度下降的方向

      # 对于Adam算法来说，如果直接将权重的平方加到loss函数上，这不是正确的
      # L2正则化（权重衰减）方法，因为这样会影响Adam中m与v的计算。
      #
      # 我们需要一种不影响m/v参数的权重衰减方法，这里讲loss的优化与L2正则
      # 分开计算，先根据Adam算法计算针对loss需要更新的量，然后加上L2正则
      # 需要改变的量.
      if self._do_use_weight_decay(param_name):
        update += self.weight_decay_rate * param     # L2正则化（权重衰减）

      update_with_lr = self.learning_rate * update    # 梯度下降的方向与量

      next_param = param - update_with_lr    # 完成梯度更新

      assignments.extend(
          [param.assign(next_param),
           m.assign(next_m),
           v.assign(next_v)])    # 保存更新操作，参数更新，梯度的一阶和二阶矩估计更新
    return tf.group(*assignments, name=name)

但optimization.py中实现的Adam算法并不是正宗的Adam算法，因为其一阶矩估计与二阶矩估计都没有校正，因为初始化时， $m_0=0,v_0=0$ ，所以刚开始的时候矩估计都有较大的偏差，所以要进行校正，运算过程中需要添加这样的计算：

$\\\\ \\beta_{1\\_t}=\\beta_1^t$ $\\\\ \\beta_{2\\_t}=\\beta_2^t$ $m_t=\\frac{m_t}{1-\\beta_{1\\_t}}\\\\$ $\\\\ v_t=\\frac{v_t}{1-\\beta_{2\\_t}}$

添加矩估计校正之后，相关的代码实现为：

  def apply_gradients_2(self, grads_and_vars, global_step=None, name=None):
    """笔者自己实现的函数，在原来实现上添加了一阶与二阶矩估计修正，实现Adam梯度更新算法"""
    assignments = []
    self.beta_1_t *= self.beta_1
    self.beta_2_t *= self.beta_2
    # 循环各个变量与梯度
    for (grad, param) in grads_and_vars:
      if grad is None or param is None:
        continue

      param_name = self._get_variable_name(param.name)    # 获变量的名字

      # 获取梯度的一阶矩估计
      m = tf.get_variable(
          name=param_name + "/adam_m",
          shape=param.shape.as_list(),
          dtype=tf.float32,
          trainable=False,
          initializer=tf.zeros_initializer())
      # 获取梯度的二阶矩估计
      v = tf.get_variable(
          name=param_name + "/adam_v",
          shape=param.shape.as_list(),
          dtype=tf.float32,
          trainable=False,
          initializer=tf.zeros_initializer())

      # 梯度的一阶矩与二阶矩估计更新
      next_m = (
          tf.multiply(self.beta_1, m) + tf.multiply(1.0 - self.beta_1, grad))
      next_v = (
          tf.multiply(self.beta_2, v) + tf.multiply(1.0 - self.beta_2,
                                                    tf.square(grad)))

      update = next_m / (tf.sqrt(next_v) + self.epsilon)   # 梯度下降的方向

      # 对于Adam算法来说，如果直接将权重的平方加到loss函数上，这不是正确的
      # L2正则化（权重衰减）方法，因为这样会影响Adam中m与v的计算。
      #
      # 我们需要一种不影响m/v参数的权重衰减方法，这里讲loss的优化与L2正则
      # 分开计算，先根据Adam算法计算针对loss需要更新的量，然后加上L2正则
      # 需要改变的量.
      if self._do_use_weight_decay(param_name):
        update += self.weight_decay_rate * param     # L2正则化（权重衰减）

      update_with_lr = self.learning_rate * update    # 梯度下降的方向与量

      # 修正一阶矩与二阶矩之后的结果
      bias = tf.sqrt(1 - self.beta_2_t) / (1 - self.beta_1_t)
      update_with_lr *= bias

      next_param = param - update_with_lr    # 完成梯度更新

      assignments.extend(
          [param.assign(next_param),
           m.assign(next_m),
           v.assign(next_v)])    # 保存更新操作，参数更新，梯度的一阶和二阶矩估计更新
    return tf.group(*assignments, name=name)

焦点新闻

Contact Us

Contact: 焦点-焦点平台-焦点中国加盟站

Phone: 13800000000

Tel: 400-123-4567

E-mail: admin@youweb.com

Add: Here is your company address

Company dynamics

NLP实战篇之bert源码阅读（optimization）

Related News

Categories

焦点新闻

Contact Us